Week 02
Basics of Neural Networks

LLMs in Lingustic Research WiSe 2024/25

Akhilesh Kakolu Ramarao

HHU

16 Oct 2024

Mathematical concepts

Scalars: single number

\[ x = 1 \]

Vectors: sequence of numbers

\[ v = \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} \]

Matrix: 2D list of numbers

\[ M = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} \]

Matrix multiplication

\[ \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} \times \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} \]

\[ = \begin{bmatrix} 22 & 28 \\ 49 & 64 \end{bmatrix} \]

Explanation:

The first matrix has 2 rows and 3 columns, and the second matrix has 3 rows and 2 columns.
The number of columns in the first matrix should be equal to the number of rows in the second matrix.
The resulting matrix will have the same number of rows as the first matrix and the same number of columns as the second matrix.
You multiply the rows of the first matrix with the columns of the second matrix.

Element-wise multiplication

\[ \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} \odot \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} \]

\[ = \begin{bmatrix} 1 & 4 & 9 \\ 16 & 25 & 36 \end{bmatrix} \]

The matrices should have the same dimensions.
The resulting matrix will have the same dimensions as the input matrices.
You multiply the corresponding elements of the matrices.

Matrix addition

\[ \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} + \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} \]

\[ = \begin{bmatrix} 2 & 4 & 6 \\ 8 & 10 & 12 \end{bmatrix} \]

You add the corresponding elements of the matrices.
The matrices should have the same dimensions.
The resulting matrix will have the same dimensions as the input matrices.

Dot product

\[ \begin{bmatrix} 1 & 2 & 3 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} \]

\[ = 1 \times 1 + 2 \times 2 + 3 \times 3 = 14 \]

The number of columns in the first matrix should be equal to the number of rows in the second matrix.
The resulting matrix will have the same number of rows as the first matrix and the same number of columns as the second matrix.
You multiply the corresponding elements of the matrices and sum them up.

Machine learning

Using learning algorithms to learn from existing data and predict for new data.
We have seen two types of Machine Learning models:
- Statistical language models
- Probabilistic language models
Today: Neural Networks

Let us say that you are given a set of inputs and outputs. You need to find how the inputs are related to the outputs.

Inputs: \(0,1,2,3,4\)

Outputs: \(0,2,4,6,8\)

You can see that the output is twice the input.
This is a simple example of a relationship between inputs and outputs.
You can use this relationship to predict the output for new inputs.

Consider a more complex relationship between inputs and outputs.

Inputs: \(0,1,2,3,4\)

Outputs: \(0,1,1,2,3\)

Can you find the relationship between the inputs and outputs?
This is where machine learning comes into play.
Machine learning algorithms can learn the relationship between inputs and outputs from the data.

Neural networks

Neural networks are a class of machine learning models inspired by the human brain.

Learning Alorithm

Neural networks learn by looking at many examples.
They adjust their internal settings (= parameters) to improve their accuracy.
This is process is called training.

Advantages of neural networks

Can learn complex patterns.
Can generalize to new data.
Can be used for a wide range of tasks (speech recognition, and natural language processing).

Architecture

The input can be a vector, and the output some classification, like a corresponding animal.

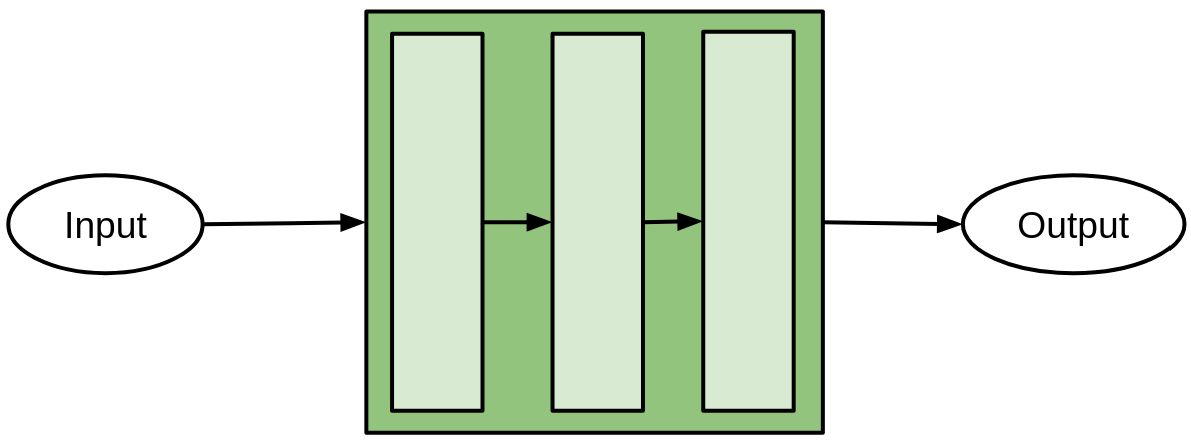Every Neural Network has Layers. They are responsible for a specific action, like addition, and pass information to eachother.

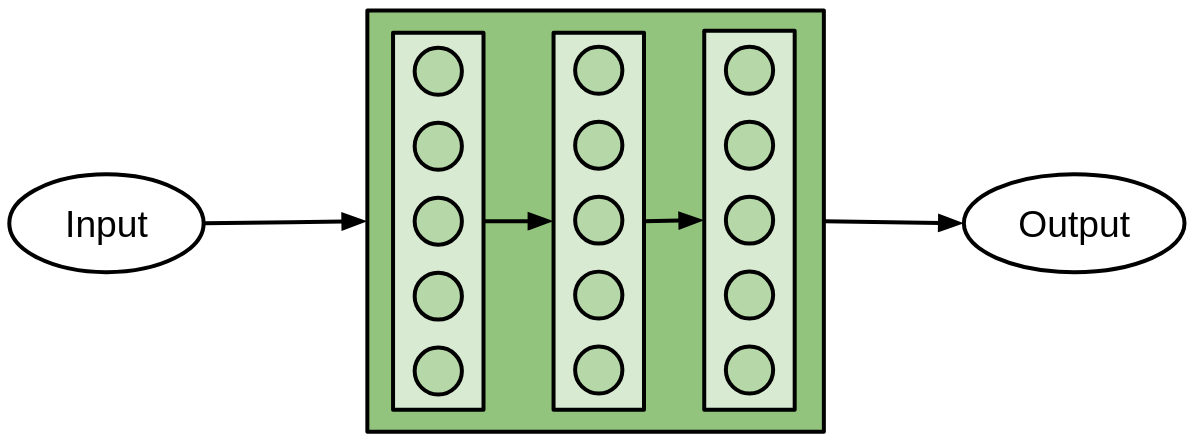Layers consist of neurons which each modify the input in some way.

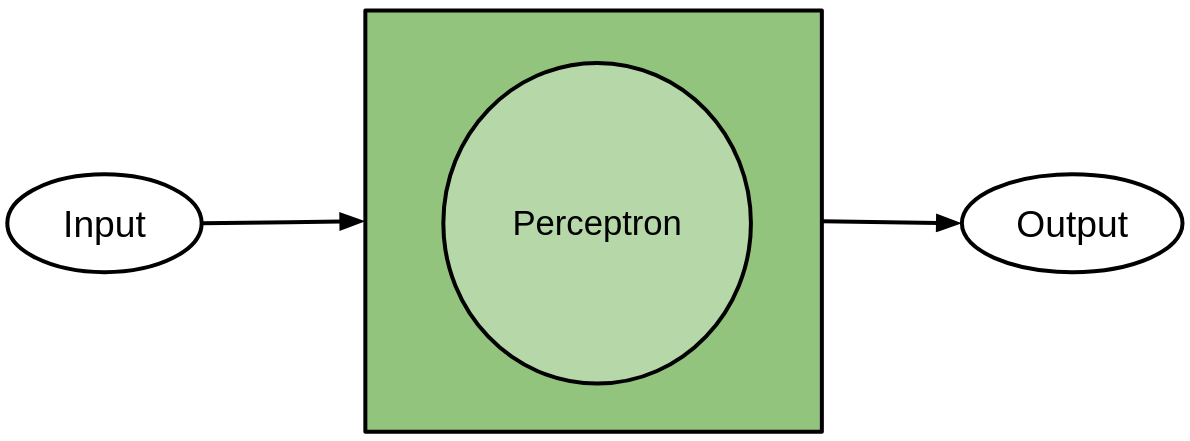The simplest Neural network only has one layer with one neuron. This is called a perceptron.

Architecture: Perceptron

graph LR
    subgraph Inputs
        x1((x1))
        x2((x2))
        x3((x3))
    end

    sum((Σ))
    act[Activation]
    out((Output))
    b[Bias]

    x1 -->|w1| sum
    x2 -->|w2| sum
    x3 -->|w3| sum
    b --> sum
    sum --> act
    act --> out

    style Inputs fill:#87CEFA,stroke:#333,stroke-width:2px, fill-opacity: 0.5
    style x1 fill:#87CEFA,stroke:#333,stroke-width:2px
    style x2 fill:#87CEFA,stroke:#333,stroke-width:2px
    style x3 fill:#87CEFA,stroke:#333,stroke-width:2px
    style sum fill:#FFA07A,stroke:#333,stroke-width:2px
    style act fill:#98FB98,stroke:#333,stroke-width:2px
    style b fill:#FFFF00,stroke:#333,stroke-width:2px

Input Nodes (x1, x2, x3): Each input is a number.
Weights (w1, w2, w3): Each weight is a number that determines the importance of the corresponding input.
Bias (b): A constant value that shifts the output of the perceptron.

Sum Node (Σ): Calculates the weighted sum of the inputs and the bias.
Activation Function (\(f\)): Introduces non-linearity to the output of the perceptron.
Output Node: The final output of the perceptron.

\[ \text{Output} = f(w_1 \times x_1 + w_2 \times x_2 + w_3 \times x_3 + b) \]

The output of the perceptron is a weighted sum of the inputs and the bias passed through an activation function.

Why do we need non-linearity?

Non-linearity allows the perceptron to learn complex patterns in the data.
Without non-linearity, the perceptron would be limited to learning linear patterns.
Activation functions introduce non-linearity to the output of the perceptron.

How does it work?

Each input (x1, x2, x3) is multiplied by its corresponding weight (w1, w2, w3).
These weighted inputs are added up with the bias (b). This is the weighted sum.

(\(w_1 \times x_1 + w_2 \times x_2 + w_3 \times x_3 + b\))

The sum is passed through an activation function.
The output of the activation function becomes the output of the perceptron.
The perceptron learns the weights and bias.
It compares its output to the desired output and makes corrections.
This process is repeated many times with all the inputs.

Additional resources

What is a neural network? [Video]

Week 02 Basics of Neural Networks